打印本文   关闭窗口

C趣味编程百例(09）歌德巴赫猜想

作者：佚名  文章来源：不详  点击数  更新时间：2008/4/18 13:59:22  文章录入：杜斌  责任编辑：杜斌

31.歌德巴赫猜想     验证：2000以内的正偶数都能够分解为两个素数之和(即验证歌德巴赫猜想对2000以内的正偶数成立)。 *问题分析与算法设计     为了验证歌德巴赫猜想对2000以内的正偶数都是成立的，要将整数分解为两部分，然后判断出分解出的两个整数是否均为素数。若是，则满足题意；否则重新进行分解和判断。     程序中对判断是否为素数的算法进行了改进，对整数判断“用从2开始到该整数的一半”改为“2开始到该整数的平方根”。原因何在请自行分析。 *程序与程序注释 #include<stdio.h> #include<math.h> int fflag(int n); void main() {     int i,n;     for(i=4;i<=2000;i+=2)     {         for(n=2;n<i;n++)         /*将偶数i分解为两个整数*/             if(fflag(n))         /*分别判断两个整数是否均为素数*/                 if(fflag(i-n))                 {                     printf("%14d=%d+%d\n",i,n,i-n);        /*若均是素数则输出*/                     break;                 }             if(n==i)  printf("error %d\n",i);     } } int fflag(int i)           /*判断是否为素数*/ {     int j;     if(i<=1)return 0;     if(i==2)return 1;     if(!(i%2))return 0;     /*if no,return 0*/     for(j=3;j<=(int)(sqrt((double)i)+1);j+=2)         if(!(i%j))return 0;     return 1;              /*if yes,return 1*/ } *运行结果

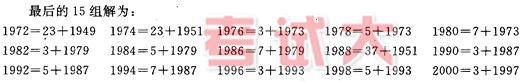
打印本文   关闭窗口