|
在本节以前给出的程序都是由一个函数组成的,实际上,一个真正的C++程序几乎都包含若干个由用户自定义的函数。
在下面的几个程序实例中,都调用了由用户定义的函数。
4.1 三次方程求根
按照Cardan公式,计算三次方程x3+px+q=0的一个实根的公式为:
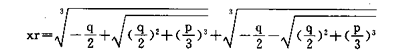
在计算实根xr的程序中,把计算一个浮点数的立方根的程序作为一个用户定义的函数,而在主程序中两次调用这个函数。
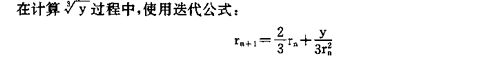
程序代码如下:
// program 4_1
#include<iostream.h>
#include<math.h>
float cuberoot(float); // 自定义函数的原型
void main()
{
float p,q,xr;
cout<<"Input paramerters p,q:";
cin>>p>>q;
float a=sqrt(q/2*q/2+p/3*p/3*p/3);
xr=cuberoot(-q/2+a)+cuberoot(-q/2-a); // 调用cuberoot函数
cout<<endl<<"The real root of the equation is "<<xr;
}
float cuberoot(float x) // 自定义函数代码从这里开始
{
float root,croot;
const float eps=1e-6;
croot=x;
do
{
root=croot;
croot=(2*root+x/(root*root))/3;
}
while(abs(croot-root)>eps);
return croot;
}
4.2 四元排序程序
对于任意的四个整数,经过处理,令其按从大到小的顺序排序。
// program 4_2.cpp
#include<iostream.h>
void swap(int &,int &); // 自定义函数原型
void main()
{
int a,b,c,d;
cout<<"Input 4 integers: ";
cin>>a>>b>>c>>d;
if(a<b)swap(a,b); // 调用自定义函数 swap()
if(b<c)swap(b,c);
if(c<d) swap(c,d);
if(a<b) swap(a,b);
if(b<c) swap(b,c);
if(a<b) swap(a,b);
cout<<endl<<a<<" "<<b<<" "<<c<<" "<<d;
}
void swap(int &x,int &y) // 自定义函数代码从这里开始
{
int temp;
temp=x;
x=y;
y=temp;
}
程序运行结果如下:
Input 4 integers: 17 25 8 41
41 25 17 8
说明:
这是一个简单的程序。函数swap()是void类型,这表明它没有返回值,所有用户定义函数都必须指明返回类型,无返回值的函数必须说明为void类型。
函数swpa()有两个整型参数,在参数表中的符号'&'表明参数x和y是“引用参数”。这与上节中的float x不同,后者称为赋值参数。引用参数和赋值参数在使用中主要有下面几点区别:
1)在形参表中增加符号'&'
2)在调用该函数时,引用参数对应的实参必须是指定类型的变量。如调用swap(a,b)中的实参a,b都是整型变量。而在上节中的赋值参数却是一个表达式,表达式的念是包含了常量、变量和一般的表达式。比如在本例中,写成swap(a+b,a-c)或swap(41,a*a+d*d)等都是错误的。
引用参数和引用调用是C++语言的一种重要功能,如果swap()的两个参数说明为赋值形参,会出现什么情况?
本例中的排序并不是一个好的方法,实际上,关于排序有很多好的算法可用。
注意:在编程中函数的作用是太重要了,不过,函数有利于编程、用利于程序结构,却不能提高程序的效率。相反,在函数调用时由于要保留“现场”以备在函数计算完成返回时继续运行原来的程序。因此,函数的每次调用,系统都要额外在时间和空间上付出一些代价。
为了解决这个问题,C++语言设置了内联函数“inline",其具体规定是:
1)在函数定义和说明之前增加关键字inline:
inline void swap(int &x,int &y){......}
2)调用内联函数与调用非内联函数的调用效果完全相同,不同的是,在对源程序进行编译时,对于非内联函数,其程序代码只有一份,在每个调用语句处,通过转移控制语句来运行,然后返回。
对于内联函数处理则不同,它是把函数体的程序代码放到每个调用该函数的语句处。例如可以把swap()函数说明为内联的:
inline void swap(int &x,int &y)
{
int temp;
temp=x;
x=y;
y=temp;
}
经过这一改动,主函数仍不变,通过编译生成的目标程序将使swap()的函数体程序代码在其中出现6次。
由此,我们可以看出,采用内联函数一方面在源程序的编写中仍可因使用函数而使程序简短清晰,另一方面在执行中又不必付出调用过程的时间和空间代价,唯一的代价是目标程序加长了。
一般说,调用次数不多的函数或函数体规模较大的函数,其调用代价相对可以忽略,不宜采内联函数。而函数体积短小且又频繁被调用的函数可以说明为内联函数。
例如对于更多个整数的排序算法,如果需要调用swap()的话,那么swap()函数应该说明为内联的。
4.3 ”三色冰激淋“程序
这是一个由冰激淋商提出来的问题,有28种颜色的原料,可以组合成多少种三色冰激淋。一种答案是有 19656=28*27*26种,称为(28,3)的排列数A 3 28 ,它是把同样三种颜色的不同排列数也计算进来了,另一答案是3276=19656/3!种,称为(28,4)的组合数。其中28为元素数,3为选择数。下面的程序对输入的元素数和选择数计算相对应的排列数和组合数。
// program 4_3.cpp
#include<iostream.h>
long factorial(int number); // 函数原型,功能计算C(m,n)=A(m,n)/n!
void main()
{
int i,selections,elements;
cout<<"Number of selections: ";
cin>>selections;
cout<<"Out of how many elements: ";
cin>>elements;
double answer=elements;
for(i=1;i<selections;i++) // 计算排列数A(m,n)=m*(m-1)*...*(m-n+1)
answer*=--elements;
cout<<"A("<<elements+selections-1<<","<<selections<<")=";
cout<<answer<<endl;
answer/=factorial(selections); // 调用factorial函数,以完成计算C(m,n)=A(m,n)/n!
cout<<"C("<<elements+selections-1<<","<<selections<<")=";
cout<<answer<<endl;
}
long factorial(int number) // 计算C(m,n)=A(m,n)/n!
{
long value=1;
while(number>1)value*=number--;
return value;
} 程序运行结果如下:
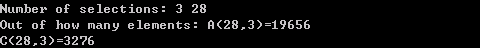
说明:这个程序中很多地方使用了复合运算符,如*=、--、++等,它们的使用有利于使程序简短、书写方便,不过应准确掌握其应用方法。
*=是赋值符与=与乘法运算符*复合而成,它是一种双止运算符,a*=b等价于a=a*b,也可以把它看作为a=a*b的简化写法。
--和++称为减量和增量运算符,属于单目运算符。a--等价于a=a-1,--a也等价于a=a-1,a--与--a的区别只有当与其它运算共同组成表达式时才能显现出来。例如answer*=--elements是一个”运算“与”乘赋值“组合成的表达式,其运算顺序是:
首先完成--elements,即elements=elements-1
然后完成answer*=elements,即answer=answer*elements
设执行之前answer=20,elements=10,则执行answer*=--elements之后,首先令elements=9,然后answer=20*9=180.
再来看一下value*=number--,运算顺序为:
首先完成 value*=number即value=value*number,
然后完成 number--.
设执行前value=20,number=10,则执行value*=number--后,首先value=20*10=200,然后number=10-1=9.
由此可以看出--a与a--;++a与a++之间的区别了。
factorial()函数也可以采用递归函数的方式设计,即在函数体内又(直接或间接地)调用该函数本身,函数定义如下:
long factorial(int number)
{
if(number<=1)return 1;
else return number*factorial(number-1);
}
这个程序与n!的数学定义式
1 n<=1
n! =
n+(n-1)! n>1
相吻合。
递归程序往往使程序思路清晰,易编易读。
|

